Wednesday 23 July 2014

Faraday's Law

Faraday's law

Question: A plane circular loop of conducting wire of radius $r=10$cm which possesses $N=15$ turns is placed in a uniform magnetic field. The direction of the magnetic field makes an angle of $30^\circ$ with respect to the normal direction to the loop. The magnetic field-strength $B$ is increased at a constant rate from $B_1=1$T to $B_2=5$T in a time interval of ${\mit\Delta}t=10$s. What is the emf generated around the loop? If the electrical resistance of the loop is $R=15\,\Omega$, what current flows around the loop as the magnetic field is increased?
 
Answer: The area of the loop is 

\begin{displaymath} A = \pi\,r^2 = \pi\,(0.1)^2 = 0.0314\,{\rm m}^2. \end{displaymath}


The component of the magnetic field perpendicular to the loop is 

\begin{displaymath} B_\perp = B\,\cos\theta = B\,\cos 30^\circ = 0.8660\,B, \end{displaymath}


where $B$ is the magnetic field-strength. Thus, the initial magnetic flux linking the loop is 

\begin{displaymath} {\mit\Phi}_{B\,1} = N\,A\,B_1\,\cos\theta = (15)\,(0.0314)\,(1)\,(0.8660) = 0.408\,{\rm Wb}. \end{displaymath}


Likewise, the final flux linking the loop is 

\begin{displaymath} {\mit\Phi}_{B\,2} = N\,A\,B_2\,\cos\theta = (15)\,(0.0314)\,(5)\,(0.8660) = 2.039\,{\rm Wb}. \end{displaymath}


The time rate of change of the flux is 

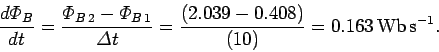
\begin{displaymath} \frac{d{\mit\Phi}_B}{dt} = \frac{{\mit\Phi}_{B\,2}- {\mit\P... ...Delta}t} = \frac{(2.039-0.408)}{(10)}=0.163\,{\rm Wb\,s}^{-1}. \end{displaymath}


Thus, the emf generated around the loop is 

\begin{displaymath} {\cal E} = \frac{d{\mit\Phi}_B}{dt} = 0.163\,{\rm V}. \end{displaymath}


Note, incidentally, that one weber per second is equivalent to one volt.
According to Ohm's law, the current which flows around the loop in response to the emf is 

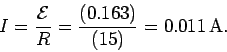
\begin{displaymath} I = \frac{{\cal E}}{R} = \frac{(0.163)}{(15)} = 0.011\,{\rm A}. \end{displaymath}
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)