The Blog Covers a lot about electrical and electronic engineering basic principles. More recent posts are now featured on www.wholebabe.info/wp/eeengtech
Thursday, 18 December 2014
Monday, 1 December 2014
Nine Advantages of Multiphase Machines over Three Phase machines.
· 1. The required current rating of the power electronic switching devices used in the inverters and converters is reduced as the number of phases increases for the same machine power rating,
· 2. The torque ripple is reduced in the multiphase machines,
· 3. Stator copper losses are reduced leading to higher efficiency,
· 4. Power per root mean square (rms) current ratio is increased,
· 5. Smaller rotor current harmonics are produced leading to more stable and reliable operation,
· 6. Multiphase machines have inherent fault tolerance,
· 7. Multiphase machines have higher power and torque density for the same machine size,
· 8. There is less interaction with the dc link current when VSI are used,
· 9. Less noise and vibrations.
Thursday, 20 November 2014
Salary Survey for Electrical Engineers in Zimbabwe
This is what I found out from the CV people Africa survey on salaries. the survey was taken from 8 practicing engineers of both genders.
The maximum salary for a highly experienced engineer is appalling.
The maximum salary for a highly experienced engineer is appalling.
Week Joke- Engineer and talking frog
An engineer was crossing a road one day, when a frog called out to him and said, "If you kiss me, I'll turn into a beautiful princess." He bent over, picked up the frog and put it in his pocket.
The frog then cried out, "If you kiss me and turn me back into a princess, I'll stay with you for one week and do ANYTHING you want."
Again, the engineer took the frog out, smiled at it and put it back into his pocket.
Finally, the frog asked, "What is the matter? I've told you I'm a beautiful princess and that I'll stay with you for one week and do anything you want. Why won't you kiss me?"
The engineer said, "Look, I'm an engineer. I don't have time for a girlfriend, but a talking frog, now that's cool."
This was taken from http://www.tickld.com/x/10-jokes-only-engineers-will-understand
There are many of these jokes on that site
Working with MS Visio - Manipulating Shapes
When you drag and drop your shapes in the page, you need to move them and position them using the guides and rules. The platform allows you to move your shapes in any way and also to resize them.
Once the shapes have been moved and joined together, you may find out that some blocks may remain behind when you move others. To get over this, you select all the blocks which you want to be always together and then you group them.
All the basics have been covered. We will then draw block diagrams in groups as given in the Visio platform. Below is a typical block diagram you can produce. Its very nice and spices up your presentation.
Keep Checking as we grow through this powerful tool.
Once the shapes have been moved and joined together, you may find out that some blocks may remain behind when you move others. To get over this, you select all the blocks which you want to be always together and then you group them.
All the basics have been covered. We will then draw block diagrams in groups as given in the Visio platform. Below is a typical block diagram you can produce. Its very nice and spices up your presentation.
Keep Checking as we grow through this powerful tool.
Tuesday, 18 November 2014
Working with MS Visio - Aligning Drawings and blocks
In many drawing applications it is difficult to properly align block. In Ms Visio, the use of rule and grids make this very simple.
Guides are even more visible than grids and rules as they draw lines on your block and you can easily align your blocks.
Next we will look at how you can move and group shapes then we will do an exemplary step by step approach. Keep checking for updates.
Guides are even more visible than grids and rules as they draw lines on your block and you can easily align your blocks.
Next we will look at how you can move and group shapes then we will do an exemplary step by step approach. Keep checking for updates.
Friday, 14 November 2014
Working with MS Visio - Connectors
After arranging your shapes in order for the program flow or chart or circuit, you uses connectors to connect the blocks.
You can make connections in the two ways shown below.
You can use auto-connect while you drag the shape
You can also use auto-connect with shapes already on the page
If you do not want to use auto-connect, you can disable it.
In the next issue we discuss how to use the Rules and Grids.
You can make connections in the two ways shown below.
You can use auto-connect while you drag the shape
You can also use auto-connect with shapes already on the page
If you do not want to use auto-connect, you can disable it.
In the next issue we discuss how to use the Rules and Grids.
Thursday, 13 November 2014
Working with MS Visio - Working with Shapes
We have introduced Visio and now its time to get into its use. Visio has a rich pack of predefined shapes that make drawing easier. The shapes are available in groups. The predefined elements are shown below
The shapes are manipulated using the handles available in visio. The handles are shown below and are used to customize the shapes.
The Shapes are contained in stenciles which group them according to applicability. However, one can use shapes from different categories.
The following diagram shows how you can navigate through the Visio interface to get the shape that you want to use.
In the next issue we look at how to connect the shapes.
Wednesday, 12 November 2014
Microsoft Visio For Perfect Diagrams and Flow Charts
Drawing good diagrams can be a challenge using Microsoft word and thank to Visio which allows the fine presentation of diagrams that can be exported or linked to MS word.
idea’s, processes, and systems.
Calendars
Timelines
Organizational Charts
Networking Diagrams
Building plans
Pert Charts
Gantt Chart
Brainstorming diagrams
Block Diagrams
Charts & Graphs
Electrical & Mechanical Engineering Diagrams
Flowcharts
Maps
Networking Diagrams
Data Base Diagrams
Business Process Diagrams
The user also has the option to create a new blank Visio Drawing and use the shapes and symbols from the above templates to create their own diagram.
What is Visio?
Microsoft Visio is a program designed to assist users in the creation and illustration ofidea’s, processes, and systems.
What does Visio do?
Through the use of Visio templates the user can create:Calendars
Timelines
Organizational Charts
Networking Diagrams
Building plans
Pert Charts
Gantt Chart
Brainstorming diagrams
Block Diagrams
Charts & Graphs
Electrical & Mechanical Engineering Diagrams
Flowcharts
Maps
Networking Diagrams
Data Base Diagrams
Business Process Diagrams
The user also has the option to create a new blank Visio Drawing and use the shapes and symbols from the above templates to create their own diagram.
The visio Interface
There are many shapes which can be used in Visio and that is our next discussion. Using Visio, you can make a state of the art presentation of figures that would require and expert is you were using MS Word.
Friday, 7 November 2014
Vector Controlled Three Phase Induction machine
The block below shows the steps and stages in implementation of Vector control in three phase induction machine. It is very important to understand the Space Vector Theory before understanding the Vector Control strategy.
Wednesday, 5 November 2014
JMAG Simulation of Rotating Magnetic Flux in Induction Motor
This video shows that poly-phase and multi-phase induction machines really produce a rotating magnetic field in the air gap. The moving magnetic field is responsible for the induction of rotor emf and resultant rotor currents.
The establishment of a rotating flux explains why the poly-phase and multi-phase induction machines are self starting.
Observe how the current density changes together with the magnetic flux density.
The establishment of a rotating flux explains why the poly-phase and multi-phase induction machines are self starting.
Observe how the current density changes together with the magnetic flux density.
Tuesday, 4 November 2014
Trapezium Rule
The trapezium rule is a method used in calculus to calculate the area under a curve. In calculus language, the area under a curve is the integral of the function defined by the curve.
The integral is given by:
Considering the figure below, it implies that the above expression can be used to get a summation of the individual are components bound by the curve. If equal widths are used, then x2-x1=Ts.
The new expression then becomes
However, Simpson's rule is more accurate when the curve is parabolic.
Monday, 3 November 2014
Tuesday, 7 October 2014
Why Scientist are not inventors
1. “...The absence of complex analytical formulas often makes easier the
concentration for the physical understanding of problems, for more lively
observation and better understanding of the substance, than when the electric
phenomena are viewed through the clouds of mathematical symbols”, Sir J.J.
Thompson, “Elements of the Mathematical Theory of Electricity and
Magnetism”.
2. “... Ignorance contributes much more frequently to self-confidence than
knowledge”, Charles Darwin, “The Descent of Man”.
3. “...Make it possible to them to invest effort and to express their ideas by
words, without the use of symbols, and if they succeed in doing so, they will
show to us that we are incapable, and they will enthusiast themselves during the
explanation, and they will even doubt that the ideas expressed may ever find the
way out of equations” James Clark Maxwell, “The Scientific Papers.”
concentration for the physical understanding of problems, for more lively
observation and better understanding of the substance, than when the electric
phenomena are viewed through the clouds of mathematical symbols”, Sir J.J.
Thompson, “Elements of the Mathematical Theory of Electricity and
Magnetism”.
2. “... Ignorance contributes much more frequently to self-confidence than
knowledge”, Charles Darwin, “The Descent of Man”.
3. “...Make it possible to them to invest effort and to express their ideas by
words, without the use of symbols, and if they succeed in doing so, they will
show to us that we are incapable, and they will enthusiast themselves during the
explanation, and they will even doubt that the ideas expressed may ever find the
way out of equations” James Clark Maxwell, “The Scientific Papers.”
Thursday, 21 August 2014
Friday Joke
A priest, a doctor, and an engineer were waiting one morning for a particularly slow group of golfers. The engineer fumed, "What's with those guys? We must have been waiting for fifteen minutes!"
The doctor chimed in, "I don't know, but I've never seen such inept golf!"
The priest said, "Here comes the green-keeper. Let's have a word with him."
He said, "Hello George, what's wrong with that group ahead of us? They're rather slow, aren't they?"
The green-keeper replied, "Oh, yes. That's a group of blind firemen. They lost their sight saving our clubhouse from a fire last year, so we always let them play for free anytime."
The group fell silent for a moment.
The priest said, "That's so sad. I think I will say a special prayer for them tonight."
The doctor said, "Good idea. I'm going to contact my ophthalmologist colleague and see if there's anything he can do for them."
The engineer said, "Why can't they play at night?"
Monday, 18 August 2014
Great Electronics Invention Helps Chinese boy to see using his tongue
A Chinese boy whose eyes were gouged out can now use a device on his tongues to see objects. watch Video on this news website
That's the power of engineering
That's the power of engineering
Engineers Joke but fact
Careers: Doctors make money from people's pain. Ministers make money from people's fears. Lawyers make money from people's mistakes. and.... Engineers make things a little bit better.
Monday, 11 August 2014
Thursday, 31 July 2014
Engineer Charming A Girl
- I won't stop bugging you until I get the address of your home.
- You fascinate me more than the Fundamental Theorem of Calculus.
- Since distance equals velocity times time, let's let velocity and time approach infinity, because I want to go all the way with you.
- My love for you is like a concave up function because it is always increasing.
Wednesday, 30 July 2014
Tuesday, 29 July 2014
Short Engineering Joke
Chief engineer: You told me that you would finish the layout in three days.
Engineer: Sure, but not three consecutive days!
The engineer then comes in to talk to his chief engineer.
Engineer: "I'm having trouble with that power supply circuit you put me to work on."
Chief engineer:"OK, let's talk about it, Is it oscillating?
Engineer: "No,it is stable."
Chief engineer:"How is the efficiency?"
Engineer: "About 87%"
Chief engineer:"Is there ringing on the gate?"
Engineer: "Nothing above normal."
Chief engineer:"What about noise and ripple?"
Engineer: "They are well within spec."
Chief engineer:"Then what's the problem?"
Engineer: "The darn thing's on fire!"
© Copyright Mark W. Lund 2008 combined with © Copyright 2013 Mark W. Lund
Engineer: Sure, but not three consecutive days!
The engineer then comes in to talk to his chief engineer.
Engineer: "I'm having trouble with that power supply circuit you put me to work on."
Chief engineer:"OK, let's talk about it, Is it oscillating?
Engineer: "No,it is stable."
Chief engineer:"How is the efficiency?"
Engineer: "About 87%"
Chief engineer:"Is there ringing on the gate?"
Engineer: "Nothing above normal."
Chief engineer:"What about noise and ripple?"
Engineer: "They are well within spec."
Chief engineer:"Then what's the problem?"
Engineer: "The darn thing's on fire!"
© Copyright Mark W. Lund 2008 combined with © Copyright 2013 Mark W. Lund
Joke- Electrical Engineering Interview
INTERVIEW
Subject: Electrical Engineering
Interviewer: Why is a thicker conductor necessary to carry a current in A.C. as compared to D.C. ?
Candidate: An AC current goes up and down (drawing a sinusoid) and requires more space inside the wire, so the wire has to be thicker.
Interviewer: How will you tell if that wall outlet carries AC or DC ?
Candidate: I will put my finger in. If it is pushed away, it is DC. If it gets stuck, it was AC.
Interviewer: How will you reverse direction of an induction motor?
Candidate: I will remove the four bolts at the base, turn the motor around, and put back the bolts.
Interviewer: How do you start a synchronous motor?
Candidate: Vrrrrrrrmmmmmmmmmmmmmmmmmmm (in rising pitch)
Interviewer: Stop! Stop!
Candidate: rrrrrrrmmmmmmmmmmmmmmmmmmmm (in falling pitch)
Interviewer: How do you limit surge current within an integrated circuit?
Candidate: By using a miniature circuit breaker.
Subject: Electrical Engineering
Interviewer: Why is a thicker conductor necessary to carry a current in A.C. as compared to D.C. ?
Candidate: An AC current goes up and down (drawing a sinusoid) and requires more space inside the wire, so the wire has to be thicker.
Interviewer: How will you tell if that wall outlet carries AC or DC ?
Candidate: I will put my finger in. If it is pushed away, it is DC. If it gets stuck, it was AC.
Interviewer: How will you reverse direction of an induction motor?
Candidate: I will remove the four bolts at the base, turn the motor around, and put back the bolts.
Interviewer: How do you start a synchronous motor?
Candidate: Vrrrrrrrmmmmmmmmmmmmmmmmmmm (in rising pitch)
Interviewer: Stop! Stop!
Candidate: rrrrrrrmmmmmmmmmmmmmmmmmmmm (in falling pitch)
Interviewer: How do you limit surge current within an integrated circuit?
Candidate: By using a miniature circuit breaker.
Monday, 28 July 2014
Magnetic Field Strength- A Level Physics
Example:
In the figure below, determine the point (other than at infinity) at which the total electric field strength is zero.

From the diagram, it can be observed that the point where E is zero lies on a straight line where the charges lie, to the left of the -2.5 μC charge.
Let this point be a distance r from the left charge.
Since the total electric field strength is zero,
E6μ = E-2μ
[6μ / (1 + r)2] / 4πεor2 = [2.5μ / r2] / 4πεor2 (Note: negative sign for -2.5 μC has been ignored here)
6 / (1 + r)2 = 2.5 / r2
√(6r) = 2.5 (1 + r)
r = 1.82 m
The point lies on a straight line where the charges lie, 1.82 m to the left of the -2.5 μC charge.
Wednesday, 23 July 2014
Faraday's Law
Faraday's law
Question: A plane circular loop of conducting wire of radiusAnswer: The area of the loop is
The component of the magnetic field perpendicular to the loop is
where
Likewise, the final flux linking the loop is
The time rate of change of the flux is
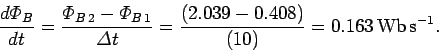
Thus, the emf generated around the loop is
Note, incidentally, that one weber per second is equivalent to one volt.
According to Ohm's law, the current which flows around the loop in response to the emf is
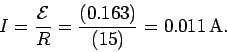
Subscribe to:
Comments (Atom)













































